Sections in this article:
How Fractals Are Used in Science and Technology.
The First Ever 3D Fractal Watch? Fractal Emergence By UnconstrainedTime.
Introduction
In this article we’ll look at what a fractal is, the discovery of fractals, types of fractals including 3D fractals, fractals in nature, how fractals are used in science and technology, fractals in the arts, other fractal watches, and this watch shown below is almost certainly the first 3D fractal watch ever made. For more info on this extraordinarily unique timepiece . . . Fractal Emergence watch – pricing and details.
What is a Fractal?
Fractals are mesmerizing and intricate geometric patterns that exhibit self-similar properties across different scales. These complex structures are found ubiquitously in nature, and also used in art, mathematics, and various scientific fields. They are characterized by their repetition, detail, and the emergence of similar patterns when zoomed in or out.
At its core, a fractal is a mathematical set that displays self-similarity, meaning that when you magnify a part of the fractal, it often resembles the whole. This property creates theoretically infinite complexity within a finite space, meaning that you could continue zooming in forever and there would still be just as much detail to see, and it would look similar to the views at other scales.
Fractional dimension is another property of fractals. If you imagine a piece of string, that has one dimension, which means one direction you can move along. If you bend the string into increasingly complex shapes, you can imagine that an infinite number of bends would completely fill a two-dimensional plane, becoming like the surface of a sheet of paper. Fractals have dimensions which are fractions, not whole numbers, such as being somewhere between a line and a flat surface, so in between one and two dimensions.
These complex shapes are often generated through iterative processes or mathematical formulas. Fractals are found in natural phenomena like snowflakes, coastlines, and trees, as well as in various fields like mathematics, science, art, and technology due to their fascinating aesthetics and relevance to how things function. More on all that, below.
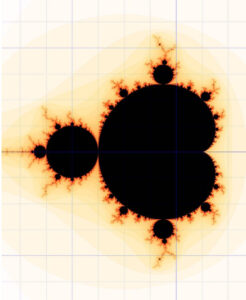
The Mandelbrot set (above), one of the most famous fractals, discovered by Benoit Mandelbrot in the 1970s, is a striking example. It is generated through a simple mathematical equation. The resulting image displays intricate and infinitely repeating patterns regardless of the scale at which it’s observed.
Fractals come in various forms, from the snowflake-like structures of the Koch snowflake to the branching patterns of trees and rivers seen in nature, all exhibiting self-similar properties. These patterns are not only aesthetically captivating but also serve as models to understand and describe the simple rules behind complex phenomena that traditional geometry cannot effectively represent.
Moreover, the concept of fractals has transcended mathematical confines, influencing art, architecture, and design. Artists often incorporate fractal patterns into their creations to evoke infinite complexity and beauty, as we will see later in this article.
In essence, fractals are captivating mathematical concepts that reveal the beauty of complexity in the world around us. Their self-similar nature and infinite intricacy not only captivate our visual senses but also offer invaluable insights into understanding, describing, and representing the complex structures we find in our universe.
The Discovery of Fractals
The discovery of fractals is credited to Benoit Mandelbrot, a mathematician who introduced this concept and its significance in the 1970s. Mandelbrot’s groundbreaking work revolutionized our understanding of geometry and provided insights into complex natural phenomena that traditional Euclidean geometry couldn’t encapsulate.
Mandelbrot’s fascination with irregular shapes led him to delve into complex mathematical patterns that occur in nature. He coined the term “fractal” from the Latin word “fractus,” meaning broken or fragmented, to describe these intricate geometric forms with properties such as self-similarity and fractional dimension, that lie on the boundaries between chaos and order.
His seminal work, “The Fractal Geometry of Nature,” published in 1982, presented a unified framework for understanding irregular shapes and structures pervasive in the natural world. Mandelbrot’s research revealed that these fractal shapes could be generated through relatively simple mathematical equations, yet they produced infinitely complex and visually stunning patterns.
The Mandelbrot set (shown above), a specific type of fractal named after him, emerged from the iteration of a seemingly straightforward mathematical formula. This set showcased the mesmerizing beauty and complexity of fractals, captivating mathematicians, scientists, and artists alike.
Fractals found applications across various disciplines. In science, they became instrumental in modeling natural phenomena like coastlines, weather formations, and the branching patterns of trees and rivers. Fractals also influenced technology, aiding in the development of computer graphics, data compression algorithms, and signal processing techniques (more on those below).
Mandelbrot’s work significantly expanded our understanding of geometry, revealing the concepts behind the prevalence of irregularity and complexity in nature. His contributions bridged the gap between mathematics and the natural world, illustrating how simple iterative processes could generate complex structures echoing those observed in our environment.
The discovery of fractals not only revolutionized mathematical thinking but also sparked new avenues of research and artistic exploration. It continues to influence diverse fields, serving as a foundation for understanding and representing the intricate beauty of the world around us.
Types of Fractals
Fractals encompass a diverse range of different types, each displaying unique properties and generating captivating geometric patterns. Here’s an overview of several prominent types of fractals:
Mandelbrot Set: As mentioned above, this was discovered by Benoit Mandelbrot, and is one of the most famous fractals.
The Mandelbrot set showcases intricate, self-similar patterns and has become an iconic representation of fractal geometry.
Julia Set:
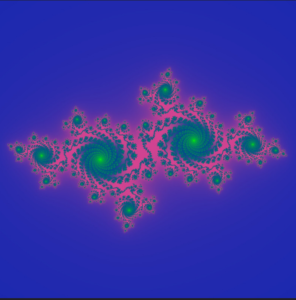
Related to the Mandelbrot set, Julia sets are also generated through complex iterative processes. Each point on the Mandelbrot set corresponds to a unique Julia set, creating a fascinating range of diverse and intricate symmetrical patterns. Our Fractal Emergence watch is based on a 3D type of Julia set.
Iterated Function Systems (IFS):
IFS fractals (including the 3D fractal above) are generated using a set of affine transformations on a geometric shape, repeatedly applying these transformations to create self-similar patterns. Famous examples include the Sierpinski triangle and the Barnsley fern. The IFS concept forms the basis of JEG image compression.
Flame Fractals:
Utilized in computer graphics, flame fractals (two of my own are shown above) are generated through an algorithm called the “flame algorithm,” creating visually stunning and colorful fractal patterns resembling flames. These fractals offer a wide range of shapes and colors, providing fascinating artistic possibilities, including being animated for use in science fiction movies (as I’ve noticed myself).
3D Fractals:
3D fractals exist in three-dimensional space. The Mandelbulb (above, right) is a notable example, discovered by using a spherical coordinate system to apply the Mandelbrot set concept to three dimensional space, resulting in intricate, volumetric fractal shapes resembling a three-dimensional version of the Mandelbrot set.
These diverse types of fractals illustrate the wide spectrum of geometric patterns and complexities achievable through iterative processes and mathematical equations. They find applications not only in mathematics and computation but also in art, design, and various scientific fields, captivating both mathematicians and enthusiasts alike with their beauty and infinite intricacies.
Fractals in Nature
Most of the natural world is made of fractals.
Fractals in nature unveil a mesmerizing tapestry of intricate patterns that repeat themselves across various scales, revealing a profound connection between mathematics and the natural world. These complex geometric structures are prevalent in countless aspects of nature, from the grandeur of mountain ranges to the delicate intricacy of snowflakes, and the leaves of an ornamental cabbage shown above.
They reveal themselves in the branching patterns of trees and ferns, the irregular shapes of coastlines, the jagged edges of lightning bolts, and the formations of clouds, fractals manifest ubiquitously. The self-similarity inherent in these natural phenomena means that when you zoom in or out, you encounter similar patterns—a hallmark trait of fractals.
The pervasive presence of fractals in nature not only demonstrates the inherent beauty of mathematical concepts but also underscores the interconnectedness between mathematics and the world we inhabit. Studying fractals in nature allows us to appreciate the elegance and complexity of our environment, while also offering valuable insights into how these systems evolve and function on both macroscopic and microscopic levels.
Fractals in nature, unlike those in mathematics, are all limited at both ends of the scale, because atoms and molecules are rarely similar to the objects they make up, and galaxies and their distribution in space have structures different from most forms at the macro and micro scales.
Coastline geometry.
The geometry of a coastline or natural border demonstrates self-similarity regardless of the scale at which it is observed, sometimes using similar patterns all the way down to the scale of grains of sand.. When measured with greater precision, the coastline appears increasingly complex, with more intricacies repeating themselves at finer resolutions. As you zoom in on a map, smaller bays and inlets replicate the larger coastline’s outline, illustrating their fractal characteristics. The same phenomena can sometimes be seen in significant differences in the stated length of the same border between two countries, when that border is defined as a natural phenomena such as a river, because the two countries measured it at different scales.
Snowflakes
. . . are another classic example, which exhibit fractal characteristics in their fascinating structures, formed by the arrangement of water molecules during crystallization. Each snowflake contains a unique pattern formed by the random accumulation of molecules, yet their intricate shapes showcase self-similarity and complex six-fold symmetry.
Fractals also appear in biological systems, such as the branching patterns of blood vessels and the intricate design of the human lung’s bronchial tubes. This repeated branching helps optimize efficiency in transport systems, allowing for maximum surface area within a confined space.
Trees and Plants:
The branching patterns of trees, ferns, and other plants demonstrate fractal properties. The self-similar structures of their branches, leaves, or roots repeat themselves as they extend, displaying complex yet consistent patterns.
I remember looking at some oak trees, fascinated by the concept that each one is a unique individual shape, yet still recognizable as an oak tree and distinguishable from others species of trees.
Mountain Ranges:
The rugged silhouettes of mountain ranges exhibit fractal characteristics in their peaks and valleys. When you examine the details of individual peaks or valleys, they echo the overall shape and structure of the entire range, whether relatively young, jagged mountains, or older, more rounded and weathered examples.
Clouds and Lightning:
Cloud formations display fractal-like shapes, with billowing forms exhibiting similar patterns at different scales.
Similarly, the jagged forks of lightning follow a fractal pattern as they branch out through the sky.
Understanding fractals in nature has broad implications. It provides insights into the underlying principles governing the formation and structure of natural phenomena. Scientists, mathematicians, and researchers use fractal geometry to model and simulate various natural processes, aiding in the understanding of ecosystems, weather patterns, geological formations, and more, as we’ll discover below.
How Fractals Are Used in Science and Technology.
Since almost all of the natural world is made of fractals, they are now starting to find numerous practical uses in science and technology.
In science, fractals are used to model irregular structures in natural systems such as coastlines, mountain ranges, and cloud formations. They also find applications in various fields like computer graphics, economics (for describing stock market behavior), medicine (analyzing brain activity and irregular heart rhythms), and signal processing.
Fractals, with their ability to model complex and irregular structures, find extensive utility across numerous scientific and technological domains, offering insights and practical applications:
Natural Phenomena Modeling:
Fractals help replicate and understand various natural phenomena such as coastlines, cloud formations, and geological landscapes. They aid in simulating and analyzing these complex systems, contributing to meteorology, geography, and geology.
Medical Imaging: In medicine, fractal analysis assists in characterizing irregular structures within biological systems. It’s applied to analyze images of organs, blood vessels, and tissues, aiding in diagnosing conditions like tumors or assessing the complexity of the vascular network.
Signal Processing:
Fractals are employed in analyzing and compressing signals due to their ability to represent intricate patterns efficiently. They enhance data compression techniques, improving signal transmission and storage.
Computer Graphics: Fractals serve as a foundation for generating realistic and visually appealing graphics. They’re used in creating landscapes, textures, and natural elements in video games, movies, and simulations, as well as many types of fractals being used as artworks in their own right (see below).
Economics and Finance:
Fractal geometry assists in modeling and understanding financial markets’ irregular behavior. It helps in analyzing stock market fluctuations, price movements, and predicting market trends.
Material Science and Engineering: Fractals aid in characterizing the surfaces of materials, understanding porous structures, and optimizing designs to enhance performance in various engineering applications like creating stronger and more efficient materials.
The adaptability and versatility of fractals have enabled their integration into numerous scientific disciplines and technological advancements, providing tools and frameworks to comprehend, model, and manipulate intricate systems in the natural world and technological landscapes.
Fractals in the Arts
While the discovery of fractals is relatively recent, fractals have, in a sense, been involved in the arts since the beginning, since most marks made by a paint brush are fractal in nature. Before abstract art, all art represented objects which could be named. The change from more than a thousand years of doing that, to abstract art is, in my opinion part of what could be called the biggest revolution in the Western Art Tradition.
Fractal art is also one of the most significant examples of mathematical art, since their beauty is a direct consequence of the mathematics underlying their creation.
Since the advent of abstract art, such marks have been presented as worthy of looking at in their own right, which also applies to the marks featured in many examples of almost-abstract art, such as Monet’s waterlilies (below) and the paintings of JWM Turner.
Fractals, once they were named as such, have made a significant impact on the arts, inspiring creativity and offering a unique avenue for artistic expression. Artists across various mediums have embraced fractal geometry for its captivating visual qualities and infinite intricacies.
Visual Arts: Fractals serve as a wellspring of inspiration for visual artists. Using fractal-generation software, artists create stunning digital artworks featuring intricate patterns and mesmerizing designs. These pieces showcase the self-similar and complex nature of fractals, producing captivating images that evoke a sense of awe and wonder.
2D Fractal images
. . . are still popular (such as the flame fractal above), after their initial surge of interest in the ’80’s. People are still creating new ones today, and sharing them in various places including dedicated Facebook Groups. I experimented with them in the fine art context, in the early ’90’s.
3D fractal images
. . . began with the Mandelbulb (detail above) in 1997, and now encompass a variety of different fractals, used as still images, video and even as 3D printed objects, an example of which we’ll see below.
Fractal videos are fascinating to watch, such as the early ones of deep zooms into mandelbrot set, Julia set and other two dimensional fractals, and now include amazing explorations of the spaces in and around 3D fractals.
Fractal-based music.
Musicians and composers utilize fractal algorithms to create innovative compositions characterized by self-similar patterns and structures. Fractal-based music explores the repetition and variation found in fractals, resulting in unique auditory experiences that mirror the complexity seen in visual fractals.
When I heard some examples of fractal music, in the early ’90’s, I was disappointed that the compositions were so “impure”, using things like MIDI notes which divided the beautiful infinite complexity of a fractal into an unrelated set of crude symbols, and piano sounds which had nothing to do with the fractal the piece was based on. I invented a much more direct way of converting a fractal into a sound, giving a much more direct and “pure” translation of the fractal into sound, which I plan to release as a sound synthesizer at some point. Here is an example of one of my pure fractal sounds: Frost3.
My approach of separating fractal sound from the limitations of notes, also fits with what could be called the biggest revolution in the Western Art Tradition.
Architecture and Design: Fractals have influenced architectural and design concepts, inspiring unconventional and organic structures. Architects integrate fractal principles into building designs, generating shapes and patterns reminiscent of fractal geometry. This approach fosters the creation of innovative and visually striking architectural marvels that echo nature’s complex forms.
An example is the fascinating fractal-like architectural pieces by Michael Hansmeyer, such as his work “digital grotesque II”, 3D printed in sandstone.
These can be seen as architecture or as . . .
Fractal Sculpture.
3D printing has made it relatively easy to physically manifest almost any object that can be modeled. Fractals are chosen by some creators and produced as sculptures. The same concepts can be applied at a smaller scale, when they become art jewelry . . .
Fractal jewelry
It has been said that the only difference between sculpture and art jewelry, is the size. The same 3D printing techniques that can make relatively small sculptures can also be used to make jewelry, often printed in precious metals like gold and platinum.
One of the best-known pieces of fractal jewelry is Marc Newson’s fractal necklace, based on a Julia set, which took 1,500 hours for craftspeople to produce.
Note that the fractal nature of forms (such as in the example above, which uses the Mandelbulb 3D fractal) and surfaces make these works art jewelry, rather than fine jewelry which is based on simple geometric shapes and smooth polished surfaces.
Fashion and Textile Design: Fractal patterns find their way into fashion and textile design, adorning clothing, accessories, and fabrics. Designers incorporate fractal-inspired motifs and shapes into their collections, offering a blend of sophistication and intricacy to garments and textiles.
Interactive Installations: Fractal-based interactive installations and exhibitions immerse viewers in a world of mesmerizing patterns and shapes. These immersive experiences engage audiences by allowing them to explore and interact with fractal art, fostering a deeper appreciation for mathematical beauty in a visual context.
The integration of fractals into the arts not only showcases their aesthetic appeal but also highlights the intersection between mathematics, technology, and human creativity. It represents a fusion of science and artistry, where mathematical principles manifest in visually stunning and thought-provoking creations.
In the same way that the choices made by the photographer show photography as an art-form, the specific aesthetic choices made from a vast array of possibilities are part of how mathematics becomes art.
Fractals continue to inspire artists to push the boundaries of creativity, providing a platform for experimentation and innovation across diverse artistic disciplines. Their beauty and complexity captivate audiences, fostering a deeper understanding and appreciation for the intricate patterns that exist within the natural world and within the realms of human imagination.
It’s interesting to consider that fractals are not the only examples of algorithmic watch design.
Other Fractal Watches
There’s only one fractal watch I can find made before ours, that I would classify as high quality. The Itay Noy Fractal collection uses a 2D fractal image on the dial of each watch.
Our watch expert, Evan says about them “the movements are especially well finished and interesting“
There are a few watches with a fractal image on the dial, available on Amazon and Zazzle. The use of fractals in watches is an example of how watches now, instead of being about functionality as they were in the past, are increasingly focusing on story and concept.
The First Ever 3D Fractal Watch? Fractal Emergence By UnconstrainedTime.
Our watch, Fractal Emergence (images below), is a 3D fractal watch, made using 3D printing (specifically, the lost wax process). The 3D fractal we used for this watch is a Julia Quaternion, which is a 4 dimensional object emerging into 3 dimensional space.
This will be the watch we launch our brand with, around April 2024.
You’ll only have one chance to buy one of the first 3D fractal watches ever made, which we’re releasing in a small limited-edition, so make sure you subscribe to our Priority List so you don’t miss our launch.
We can’t find any examples of 3D fractal watches before ours, so we believe ours is the first ever 3D fractal watch! If you know differently, tell us below, or on our social media. And we’d love to know what you think of our Fractal Emergence watch.
Leave a Reply